4月に入り大学の授業も始まりました.新入学生が苦労する「線形代数」の全体像や学習の流れについてお話しします.(大学1年,高専2,3年で学ぶ程度の線形代数についてです.)
はじめに
線形代数は,理系・経済系の大学生の学部1年,工業高専の2,3年の必履修科目になっていることが多い科目です.(高等学校では,2003年度施行の「数学C」において理系選択の多くの生徒が行列の基礎事項を学んでいましたが,2012年度施行の指導要領では「数学C」が廃止され,行列の内容が含まれた「数学活用」や「理数数学特論」(理数科の科目)においても現在はほとんど扱われなくなっています.)そして,履修する人の多くが途中からついていけなくなる科目でもあります.この記事では,線形代数の意義や全体像を把握することで,学習のモチベーションを高めるとともに,習得しやすくすることが目的です.初学者向けの記事のため,大まかに述べています.
なぜ線形代数をやるのか
まず知っておいて欲しいのは,線形代数はものすごく色々な分野に応用・活用されているということです.もちろん,分野によって活用する内容は異なります.
数学系では,線形代数の内容の全てが数学の基礎となっています.詳しくは後で述べますが,線形代数で学ぶ「行列」「ベクトル空間(線型空間)」「線型写像」などは,それ自体面白い性質を持った対象です.行列を直接応用する例としては,群などの代数系の性質を行列を使って調べようとする「表現論」などがあげられます.具体的に応用する側面もあれば,全ての数学分野の根本になっている概念を学ぶという側面が強いです.
物理系では,力学などで多次元の物体の運動を記述するのにもベクトルや行列の知識は必須です.また量子力学でも行列やベクトルを用いて体系づける,記述することが主流になっています.
経済系では,経済波及効果の検証など,多くのデータを分析するための計算手法として,行列が使われることが多いらしいです.後で述べますが,行列は連立方程式の計算を統一的に行う(1本の方程式として扱う)ために作られた側面のあるので,これは自然な応用例です.
他にも,今流行りの機械学習やデータ解析などにも,線形代数の知識が応用されています.このように,線形代数は,どの分野においても応用される,基礎的な科目です.
学習の流れと全体像
さて,現在の高等教育機関で行われている線形代数の授業の,一般的な流れを説明します.理学部数学科,理学部の非数学科,工学部,高専,その他では,扱う内容に多少の差があるかもしれませんので,シラバスや指定教科書も参考にするといいと思います.また,詳細の説明は教科書等に譲り,ここでは大まかな説明で雰囲気が分かる程度に留めます.
ベクトル
高等学校で学んだベクトルは,「移動可能な有向線分」をベクトルと定義して,(これがちゃんと定義されているかは置いておいて,)その図形的な意味を学んだり,和とスカラー倍を定義して基本的な計算を行っていました.このベクトルのことを,通常は「幾何ベクトル」と言います.すなわち,2次元の平面 \( \mathbb{R}^2 \) や3次元空間 \( \mathbb{R}^3 \) で矢印としてイメージできるベクトルです.(高専では,幾何ベクトルから学び始めます.)
まずはこの幾何ベクトルのイメージのままで良いので, \( \mathbb{R}^3 \) 内の直線や平面の方程式がどのように表されるのかを学びます.この証明には,内積や外積などの概念を使うことがあるので,その定義やイメージも学びます.高校までに平面 \( \mathbb{R}^2 \) での直線の方程式を勉強したので,これは自然な流れです.
その後,さらに一般に,成分として数字を n 個並べたベクトルとその演算を定義します.和やスカラー倍,内積,外積などは同じように定めます.2,3次元の空間とは違う点は,図形的なイメージができないところです.このように定めたベクトルを通常は「数ベクトル」と言います.これからは,このベクトルを扱っていきます.幾何ベクトルのような矢印のイメージを脱却して, n 個の数字を並べた数ベクトルの感覚を掴むことが大切です.
行列の計算
ベクトルの内容が習得できたら,行列を学びます.行列はその名の通り,数字を行と列に並べたものです.行列にも和やスカラー倍,さらに行列の積を定義します.実はベクトルも行列の一部なので,(一定の条件下で)ベクトルと行列の積も定義されたことになります.
行列の積で注意すべき点は,積が可換ではない(非可換である)ことです.すなわち,一般にAB≠BAであることです.そのため,「左からかける」「右からかける」を区別する必要があります.
行列の積を使って,ベクトルを違うベクトルに変換することができるようになります.例えば,実数の世界なら,3に4/3倍したら4になります.同じように,ベクトル
\begin{pmatrix} 1 \\ 2 \end{pmatrix} に
\begin{pmatrix} -1 & 3 \\ 4 & 5 \end{pmatrix} 倍する(左からかける)と\begin{pmatrix} 5 \\ 14 \end{pmatrix} になります.このように,行列は,ベクトルをベクトルに変換する役割を持っています.
連立1次方程式
行列の応用の最も基本的なものが,連立1次方程式の解法です.例えば,連立一次方程式
\[\begin{eqnarray} \left\{ \begin{array}{l} x + 2y = 10 \\ 3x + 4y = 15 \end{array} \right.\end{eqnarray}\]
は,行列を用いて,
\[\begin{eqnarray} \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 10 \\ 15 \end{pmatrix} \end{eqnarray}\]
と表されます.連立方程式を解く時に使う加減法はいちいち式を書くのが面倒なので,係数の部分の行列(係数行列)と右辺のベクトルを合わせた拡大係数行列を考えて,加減法に対応する操作をできるようにします.これを,行基本変形と言います.行基本変形をして,拡大係数行列をできるだけ簡単な形にして連立方程式の解を求める方法を「掃き出し法」や「ガウス(・ジョルダン)の消去法」と言います.この方法を求める際,解が一意に定まるか,不定の解が求まるか,解がないかは,拡大係数行列の性質に依存します.どのような依存性があるのかを主に学びます.詳しく言えば,拡大係数行列のrank(ランク,階数)と係数行列のランクが一致していれば解が存在します.また,そのrankが未知数の個数と一致していれば,解は一意に定まります.
このような理由から,行列のrankや行基本変形について勉強します.
また,行基本変形は逆行列(行列の積に関する逆元)を求める際にもよく用いられます.実は,後で勉強する「余因子行列」や「行列式」を用いて逆行列を求める公式が存在します.しかし,その公式を用いて計算するより行基本変形を用いて計算する方が計算量が少ないことが知られています.(一方で,公式は行列の成分などを用いて明示的に計算できるので,コンピュータに計算させる時によく用いられます.)
行列式
行列式とは,正方行列(行と列の本数が同じ行列)それぞれに対して1つ定まる量(実数)であり,幾何的な意味や特有の性質を持つものです.行列式の定義は少し難しく,工学部などの非数学科では定義をしっかり学ぶことはあまりありません.実際に求める際は,2次や3次の場合は簡単な計算法(サラスの方法)があるので普通はそれを用います.4次以上になるとこの計算法は使えないので,行基本変形(これによって行列式がどうなるかも学びます)や行列式の展開(余因子展開)などを使って工夫をし,3次以下の行列式の計算に帰着させる方法がよく使われます.
さて,行列式の意味ですが,2次元の実ベクトル \(a,b \in \mathbb{R}^2 \) を横に並べた行列(これは2次の正方行列)の行列式 \( det(a b) \)の絶対値\( |det(a b)| \)は,平面上で2本のベクトル\(a,b \)が張る(作る)平行四辺形の面積と一致します.
また,3次元の実ベクトル \(a,b,c \in \mathbb{R}^3 \) を横に並べた行列(これは3次の正方行列)の行列式 \( det(a b c) \)の絶対値\( |det(a b c)| \)は,3次元空間上で3本のベクトル\(a,b,c \)が張る(作る)の並行六面体の体積と一致します.
さらに,行列式は幾何的な意味を持つだけではありません.実は,行列Aの行列式が0でないことと,Aの逆行列が存在する(すなわちAが正則である)ことは同値です.実際,先ほど少し述べた逆行列の公式の分母に行列式が含まれています.この事実を用いて,Aの逆行列があるかを判別することもあります.
このように,各正方行列に対して定まる,特殊な性質を持った実数が行列式です.
ベクトル空間(線型空間)
この内容から,さらに抽象的になっていきます.今まで扱ってきた集合は\( \mathbb{R} \)や\( \mathbb{R}^n \),\( \mathbb{C} \)には,全て「和」「スカラー倍」という演算が組み込まれていました.このような構造を一般的に定義しておきます.
(雑な定義)集合Vがk上のベクトル空間(線型空間)であるとは,Vが以下の条件を満たすときを言う.(kはスカラーの集合.よく\( \mathbb{R} \),\( \mathbb{C} \)が用いられる.)
(I)和について閉じている(Vの元(要素)同士の和も,Vの元である.)
(II)スカラー倍について閉じている(Vの元にスカラー(kの元)をかけたものも,Vの元である.)
(III)和とスカラー倍について,以下が成り立つ.
(1)Vの元の交換法則が成立.
(2)Vの元の結合法則が成立.
(3)零元が存在する.
(4)和についての逆元がある.
(5)スカラー倍の分配法則が成立.(2種類)
(6)スカラー倍の結合法則が成立.
(7)スカラー倍の単位元1が存在する.
(ここでは簡単に書いたので,詳しくは教科書を参照して下さい.kは\( \mathbb{R} \)や\( \mathbb{C} \)に,Vは\( \mathbb{R}^n \)に読み替えてもらっても良いです.)
(I)と(III)の(1)〜(4)は言い換えれば,Vは和に関して可換群である,(III)の(5)〜(8)は,和とスカラー倍に整合性があるということです.
今まで扱ってきた\( \mathbb{R} \)(実数全体の集合),\( \mathbb{C} \)(複素数全体の集合)などが,普通の和とスカラー倍に対して上を満たすことは,少し考えれば分かるでしょう.また,\( \mathbb{R}^n \)(n個の実数を並べたもの全体の集合)に,「成分同士で和をとる」という和と,「各成分をスカラー倍する」と言うスカラー倍を用意すると,それによって\( \mathbb{R}^n \)はベクトル空間になります.
実はこれ以外にもベクトル空間である集合はたくさんあります.例えば,高々n次の多項式全体の集合 \( P_{n} = \{a_nx^n + a_{n-1}x^{n-1} + \cdots +a_1x + a_0 | a_0 , \cdots a_n \in \mathbb{R} \} \)は,式としての通常の和とスカラー倍で,ベクトル空間となります.
一般に,ベクトル空間の元(要素)のことを「ベクトル」といいます.そのため,一番初めに勉強した”ベクトル”(\( \mathbb{R}^n \)の元)だけでなく,もっと広い意味でベクトルという言葉を使うことがあるのです.
次に,ベクトル空間の部分空間について勉強します.ベクトル空間の部分空間とは,ベクトル空間の部分集合であり,同じ演算によってそれ自体もベクトル空間であるもののことです.(ちなみに,数学において一般に,何かの演算によって構造を組み込んだ集合のことを「空間」と言い,その部分集合で同じ構造を持つものを「部分空間」いうことが多いです.「空間」の代わりに異なる用語「〇〇」なら,「部分〇〇」ということが多いです.)
工学部などでは一般的なベクトル空間を考えることはあまりなく,ベクトル空間\( \mathbb{R}^n \)の中だけで考えることが多いです.そのため,一般のベクトル空間については詳しく勉強しないことが多いです.
ベクトル空間に内積の構造も入れた,計量線型空間というものがあります.\( \mathbb{R}^n \)のベクトルの内積については高校でも学びますが,一般のベクトル空間については内積の公理というもので定めます.この内容も,工学部ではあまり学びません.
線型写像
ここでは,写像(関数の一般化だと思って下さい.数学の中で最も大切な概念なので,勉強して下さい.)の中でも美しい性質を持った「線型写像」を勉強します.
(雑な定義)k上のベクトル空間V,Wに対して,\( f:V \to W \)が線型写像であるとは,以下を満たしている時をいう;
\( x,y \in V \),\( a \)をスカラーとすると
(I)\( f(x+y)=f(x)+f(y) \)
(II)\( f(ax)=af(x) \)
もしくは,\( x,y \in V \),\( a,b \)をスカラーとして
(I’)\( f(ax+by)=af(x)+bf(y) \)
と言っても同じ事である.
この性質を線形性といいます.すなわち簡単に言えば,線型写像とは線形性を持った写像です.線形性のイメージは以下の記事に書いているのでご覧ください.
線型写像の例として,一番初めのベクトルで学ぶであろう,ベクトルの回転や鏡映,相似変換は,実は線型写像です.
そして,驚くべきことは,ベクトル空間V,Wの基底(線型独立でその空間を張るもの,簡単に言えば基準)を決めてやることで,線型写像\( f:V \to W \)が一つの行列と対応する(線型写像を行列で表せる)のです.これを,(Vの基底〇〇,Wの基底△△に関する)表現行列といいます.
他にも,次元公式などの重要事項を勉強します.このようなことを学ぶために,線型写像を学ぶ前に行列やベクトル空間と部分空間について学ぶのです.
固有値と固有ベクトル
この内容は,もしかしたらベクトル空間や線型写像の前に学ぶかもしれません.
(定義)n次正方行列\(A\)に対して,\( Ax=\lambda x (x \neq 0 ) \)を満たすスカラー\( \lambda \)を\(A\)の固有値,\( x \in \mathbb{R}^n \)を\( \lambda \)に対応する固有ベクトルという.
n次正方行列\(A\)に対して,\(Ax \in \mathbb{R}^n \)は一般に\(x \in \mathbb{R}^n \)とは別の方向を向くベクトルですが,それが特に\(x \)のスカラー倍(延長線上のベクトル)であるような特別なベクトル\(x \)とその延長率\( \lambda \)の組のことを,固有ベクトル,固有値というわけです.
この内容は,次に説明する「行列の対角化」に利用します.また,力学や量子力学など,物理の分野にも幅広く応用されている内容です.一般に,固有値や固有ベクトルを求める問題のことを「固有値問題」といいます.
行列の対角化
行列の対角化とは,考える正方行列A(n次正方行列としましょう)にある行列を左右からかけて,対角行列にしようという試みです.これは,全ての行列に対して可能というわけではなく,特定の条件下で可能です.(具体的には,Aの固有ベクトルがn個の線型独立な固有ベクトルを持っている時のみ可能です.)
なぜ対角化をするのかというと,対角行列は非常に扱いやすい行列だからです.例えば,単位行列Eは,行列の積における単位元(実数で言うと1のような性質を持つもの)であるし,対角行列をかけることにおいては計算が楽です.また,一般に行列\( A \)のn乗\( A^n \)を計算するのは非常に厄介ですが,対角行列のn乗であれば簡単です.(実際にやってみて下さい.)そのため,対角行列にするという試みは自然なことなのです.
この内容は,Aの固有値と固有ベクトルを用いるため,上の「固有値と固有ベクトル」を学んだ直後に学ぶことがほとんどです.
ジョルダン(Jordan)標準形
この内容は,工学部で学ぶことはあまりないのかもしれません.
上で説明した「行列の対角化」は,どんな正方行列に対してもできるわけではありません.そのため,もし対角化できなくてもそれに近い簡単な形にできないか,という試みをします.「ジョルダン標準形」というできるだけ簡単な形にしようという理論を学びます.具体的にジョルダン標準形にすることはそこまで難しくないですが,実現する方法を理論的に示そうと思うととても難しい内容になってしまいます.そのため,理論は数学科でしか学ばないと思います.
オススメ参考書と学習法
学習法
まず勉強法についてですが,やはり他の数学の分野と同じように,定義をしっかり覚えて,具体例で感覚を掴み,定理をしっかりと証明して理解することが必要です.特に,高専生も大学生も,これまでやったことがない内容なので,具体例でたくさん計算することが大切です.また,証明の仕方などは,代数特有の考え方を多く使います.線形代数の定理などで証明に慣れることができれば,抽象的な代数においても証明がやりやすくなると思います.
線形代数の教科書や参考書はとても種類があります.その中でも用途に合わせて厳選すると以下の通りです.
教科書・参考書
数学科の教科書にの指定されることもある正統派の教科書です.細かく書いており,辞書としても使えます.大学院入試を受ける人や,数学科の人にはおすすめです.しかし,初学者には向きません.
圧倒的シェアを誇る参考書です.噛み砕いて説明してくれるので,初学者にはとてもおすすめです.これさえあれば,定期テストや工学系の院試まで乗り切れるとも思います.大学生向けですが,高専生にもおすすめです.
この本はあまり知られていませんが,演習書としてとても推していきたい1冊です.例題と解答が豊富であり,教科書では補えない問題の演習ができます.解答が親切なので,理解が深まります.定期テストや大学院入試,大学編入試験など,様々な用途で使えます.
あまり知られていないのですが,大学の初学者で理解に困っている人には,高専の教科書をおすすめします.なぜなら,高校の教科書と同じような体裁で書いてあり,例題や演習問題も豊富で自学しやすいためです.(ただし,ベクトル空間などの細かいことは紹介されておらず,非数学科向けです.)
高専の教科書です.この本は参考書と同じくらい細かく紹介されています.コラムなどでベクトル空間のことも書いてあり,正直この本を工学部の教科書にしても良いとさえ思います.
高専の教科書です.上の本よりさっぱりと書かれていますが.ごちゃごちゃしていないところが良いです.このくらいさっぱりでも理解するのには全く問題ないと思います.しかし,内容が上の本より若干少なく,大学生が参考書として使うには物足りないかもしれないです.
さいごに
ここまで見てくださってありがとうございました.線形代数は大学1年や高専2年生がつまずきやすい分野の一つです.この記事が,何をやっているか分からない,雰囲気をつかめていない人に参考になればと思います.
関連記事

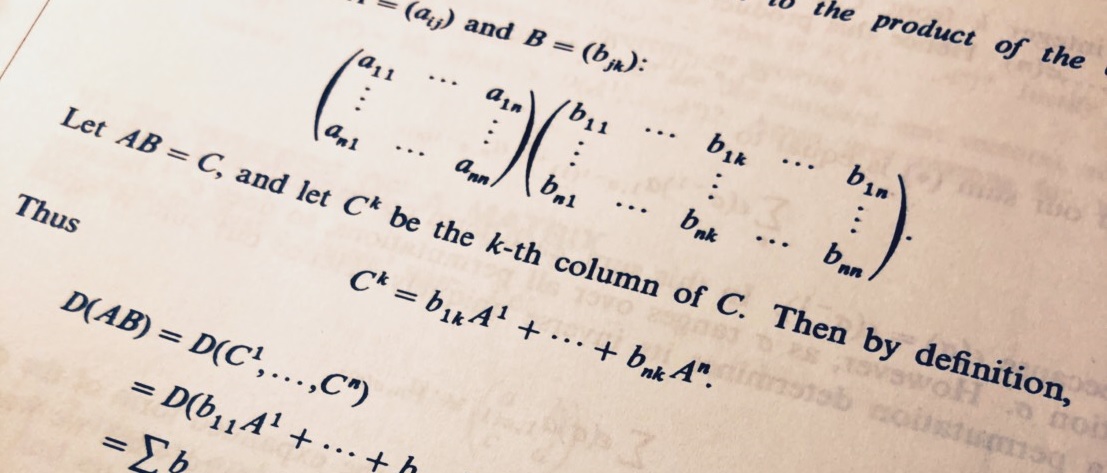






















コメント