最近,確率分布についての授業をする機会があったので,何回かに分けて,二項分布とポアソン分布についての簡単な知識とそれらの関係性について述べていきます.今回は確率分布の基礎と二項分布についてみていこうと思います.
確率変数と分布
まず今回の話の基礎である,確率変数と分布について簡単に述べておきます.
確率変数とは,簡単にいえば,「ある試行の結果によって値が決まる変数で,各値をとる確率が定まっているようなもの」のことです.
例えば,1つのサイコロを振ったときに出た目を$X$とします.このとき$X$は確率変数になっています.なぜなら,「1つのサイコロをふる」という試行によって$X$の値が1以上6以下の整数の1つだけ決まり,しかもそれらは全て確率$1/6$と定まっています.$X=k$になる確率を$P(X=k)$と書くことにすると,この場合は$$P(X=k)=\frac{1}{6} \quad (k=1, \cdots ,6)$$です.このように確率変数のとり得る値が整数のようにとびとびの値であるとき,特に離散型確率変数といいます.
もちろん,この$P(X=k)$は等確率でないこともあります.例えば,2枚のコインを投げて表が出る枚数を$X$とすると,$X$がとり得る値は$0,1,2$であり,$$P(X=0)=\frac{1}{4}, \quad P(X=1)=\frac{1}{2}, \quad P(X=2)=\frac{1}{4}$$です.
そして確率分布とは,確率変数のとり得る値と,その値をとる確率の情報のことをいいます.すなわち,先程の例のように,確率変数$X$のとり得る値とその確率$P(X=k)$が全て分かっているとき,確率分布が分かっているということです.
二項分布とその性質(平均,分散)
さて,ここで次のような状況を考えてみましょう.1つのサイコロを5回投げるとき,3の倍数が出る回数を$X$とすると,$X=2$となる確率$P(X=2)$はどのようになるでしょうか.これは,素直に考えれば容易で,1回投げて3の倍数が出る確率は$1/3$ですから,5回中2回これが起こる確率は「反復試行の確率」で求められ,$$P(X=2)={}_5 C_2 \left( \frac{1}{3} \right)^2 \left( \frac{2}{3} \right)^3$$ですね.これをもう少し一般的に表記してみましょう.
まず前提として,上の例のように反復試行で考える必要があるので,試行の条件として「繰り返し行ってもそれぞれの起こる確率が変わらない」ことが要請されます.これを満たし,結果が「成功」か「失敗」(「yes」か「no」と考えても良い)の2パターンしかない試行をベルヌーイ試行といいます.
ベルヌーイ試行を$n$回繰り返すことを考えます.1回の試行において事象$A$が起こる確率を$p$とします.(ベルヌーイ試行なのでこの値は常に一定です.)そして,事象$A$が起こる回数を$X$とします.このとき$X$は$0,1,\cdots,n$の値をとり得る確率変数になっています.$k=0,1,\cdots,n$に対して,$X=k$となる確率$P(X=k)$は,反復試行の確率から$$P(X=k)={}_n C_k p^k \left( 1-p \right)^{n-k}$$です.
ここで1つ疑問に思うのは,これが本当に確率として正しいのか?ということです.どういうことかというと,確率は0以上の値であって,総和が1でないといけません.それを本当に満たしているのでしょうか.それを確認してみましょう.まず,各$k$に対して,$$P(X=k)={}_n C_k p^k \left( 1-p \right)^{n-k}$$の値が0以上であることはすぐに分かりますね.そして,総和が1かという点については,$$\sum_{k=0}^n {}_n C_k p^k \left( 1-p \right)^{n-k}=(p+(1-p))^n=1^n=1$$より満たしています.ここで,1つ目の等式は二項定理を用いました.
このような状況のとき,この確率変数$X$は二項分布(もしくはベルヌーイ分布)に従う,といいます.さらに詳しくいうと,決められた事象$A$(このとき確率変数$X$も決まる)に対して,二項分布は$n,p$で決定されるので,それをあらわに書いてこの二項分布を$B(n,p)$と表します.すなわち,$X$は$B(n,p)$に従う,といいます.
先ほど述べた例は,ベルヌーイ試行が「1つのサイコロを繰り返し投げる」,事象$A$が「サイコロを投げて3の倍数が出る」,$n=5$,$p=1/3$に対応していますね.すなわち,3の倍数が出る回数$X$は$B(5,1/3)$に従っています.
それでは,この二項分布$B(n,p)$の性質について考えていきましょう.
まず平均(期待値)を計算します.確率変数$X$の確率分布の平均(期待値)$E[X]$の定義は次の通りです.
確率変数$X$のとり得る値が$x_1, \cdots ,x_n$で,各値をとる確率が$P(X=k)=p_k \quad (k=1, \cdots ,n)$であるとき,
$$E[X]=\sum_{k=1}^n x_kp_k$$
でしたね.これを用いて$B(n,p)$に従う確率変数$X$の平均を真面目に計算すると,$$E[X]=np$$であることがわかります.
$q=1-p$とする.先ほどのcommentのところで出できた式のように,二項定理から,$$\sum_{k=0}^n {}_n C_k p^k q^{n-k}=(p+q)^n$$がわかる.この式の両辺を(形式的に)$p$で微分してみると,$$\sum_{k=0}^n k{}_n C_k p^{k-1} q^{n-k}=n(p+q)^{n-1}$$となる.両辺を$p$倍すると,$$\sum_{k=0}^n k{}_n C_k p^{k} q^{n-k}=np(p+q)^{n-1}=np$$である.($p+q=1$を用いた.)この式の左辺はまさに,$E[X]$であるから,$E[X]=np$である.
また,分散も計算してみます.確率変数$X$の確率分布の分散$V[X]$の定義は次の通りです.
確率変数$X$のとり得る値が$x_1, \cdots ,x_n$で,各値をとる確率が$P(X=k)=p_k \quad (k=1, \cdots ,n)$,平均が$\mu$であるとき,
$$V[X]=\sum_{k=1}^n (x_k-\mu)^2 p_k$$
(もちろん,定義から$V[X]=E[(X-\mu)^2]$である.)
でしたね.これを用いて$B(n,p)$に従う確率変数$X$の分散を計算すると,$$V[X]=np(1-p)=npq$$であることがわかります.
平均の計算のところで現れた$$\sum_{k=0}^n k{}_n C_k p^{k-1} q^{n-k}=n(p+q)^{n-1}$$の両辺をもう一度$p$で(形式的に)微分すると,$$\sum_{k=0}^n k(k-1){}_n C_k p^{k-2} q^{n-k}=n(n-1)(p+q)^{n-2}$$である.両辺に$p^2$をかけて,$$\sum_{k=0}^n k(k-1){}_n C_k p^{k} q^{n-k}=n(n-1)p^2(p+q)^{n-2}=n(n-1)p^2$$である.ここで左辺は,和を分配することにより,$$\sum_{k=0}^n k(k-1){}_n C_k p^{k} q^{n-k}=\sum_{k=0}^n(k^2-k){}_n C_k p^{k} q^{n-k}=\sum_{k=0}^n k^2{}_n C_k p^{k} q^{n-k}-np$$である.よって,$$\sum_{k=0}^n k^2{}_n C_k p^{k} q^{n-k}=n(n-1)p^2+np$$が分かった.
また,$V[X]=E[X^2]-E[X]^2$という性質(これは容易に証明できます.)を用いれば,$$V[X]=\sum_{k=0}^n k^2{}_n C_k p^{k} q^{n-k}-(np)^2=n(n-1)p^2+np-(np)^2=np(1-p)$$である.
二項分布に従う確率変数の例
二項分布の具体例をいくつか紹介します.
例1:コインを4回投げて,表が出る回数を$X$とする.このとき,1回の試行で表が出る確率は1/2なので,$k=0,1,2,3,4$に対して,$$P(X=k)={}_4 C_k \left( \frac{1}{2} \right)^k \left( \frac{1}{2} \right)^{4-k}$$である.よって,$Y$は二項分布$B(4,1/2)$に従う.ちなみにこの分布の平均(期待値)は$E[X]=2$なので,「コインを4回投げて結果を観測」をたくさん行うと,4回投げるあたり$2$回表が出ると期待されるということである.
例2:白玉2個,赤玉7個の入っている袋から1個ずつ3回復元抽出する.(取り出した玉を毎回戻して試行を繰り返す.)白玉が出る回数を$Y$とする.このとき,1回の試行で白玉が出る確率は2/9なので,$k=0,1,2,3$に対して,$$P(Y=k)={}_3 C_k \left( \frac{2}{9} \right)^k \left( \frac{7}{9} \right)^{3-k}$$である.よって,$Y$は二項分布$B(3,2/9)$に従う.ちなみにこの分布の平均(期待値)は$E[Y]=2/3$なので,この復元抽出をたくさん行うと,3回復元抽出するあたり$2/3$個白玉が出ると期待されるということである.
さて,これらの例に対して,$X=k$や$X \le k$となる確率などを計算したいとしましょう.
例1において,例えば$X \le 1$である確率$P(X \le 1)$を計算しようと思ったら,$$P(X \le 1)=P(X=0)+P(X=1)={}_4 C_0 \left( \frac{1}{2} \right)^0 \left( \frac{1}{2} \right)^{4}+{}_4 C_1 \left( \frac{1}{2} \right)^1 \left( \frac{1}{2} \right)^{3}$$を計算すれば良いです.この場合は計算が結構簡単で,$$P(X \le 1)=P(X=0)+P(X=1)=\frac{5}{16}$$となりますね.
しかし,例2において,例えば$Y \le 1$である確率$P(Y \le 1)$を計算しようと思ったら,$$P(Y \le 1)=P(Y=0)+P(Y=1)={}_3 C_0 \left( \frac{2}{9} \right)^0 \left( \frac{7}{9} \right)^{3}+{}_3 C_1 \left( \frac{2}{9} \right)^1 \left( \frac{7}{9} \right)^{2}$$を計算すれば良いですが,この計算は(もちろん真面目に計算して出すことはできますが,)意外と厄介ですね.
この例2からもわかるように,二項分布では,理論的には計算できるが,実際に計算するのが大変という状況に出会う場面があります.実はこのような場合,次回解説するポアソン分布という分布に近似させて計算するという手法が使えます.この近似は特定の状況下でしか行えませんが,手軽に計算できるという観点で重要です.





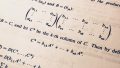

コメント