今回は,大学で学ぶ数学の中でも,整数論,特に代数的整数論に関するおすすめの本を紹介します.整数論は,よく「初等整数論」「代数的整数論」「解析的整数論」の3つに分類されます.(私の感覚では,この順に難しくなっていきます.)もちろんそれぞれが独立しているのではなく,必要な基礎知識や考え方の発想などにより,大まかに区別されているだけです.正直私も,どこまでが初等整数論か,などの分類がはっきり分かっているわけではありません.ちなみに私は,代数的整数論の知識を前提とする類体論という分野を勉強しています.
初等整数論は,基本的にはあまり難しい前提知識を必要とせず,パズルのように考えていくようなイメージがあります.初等整数論の本はほとんど前提知識が必要ないので,初学者や整数論に興味のある人はここから始めると良いでしょう.群・環・体などの知識がなくても,読めると思います.(群・環・体などの知識を用いる場合は,そこでしっかり定義してくれていると思います.同時期に勉強すると,相互的に理解が深まるかもしれません.)また,本によっては,代数的整数論の入門の位置付けで書いてある本もあります.
代数的整数論は,代数学の知識を前提として,論理を展開していきます.ここで扱う「整数」とは,$0, \pm 1,\cdots $のようなものだけでなく,「代数的整数」というものです.代数的整数とは,整数係数のモニック多項式(最大次数の係数が1である多項式)の根のことです.例えば,$\sqrt{2}$は$x^2-2$の根なので代数的整数です.詳しくはここでは省略しますが,このような数(のなす代数構造)の性質を調べていくのが代数的整数論です.「代数的」な整数論ではなく,「代数的整数」の論と思う方がしっくりきます.
解析的整数論は,主に解析学の手法(微積分など)を用いて整数論を展開していきます.高度な解析学の手法を前提知識として要求されます.素数の分布を理解する素数定理などは,この分野に含まれると思います.また,リーマン予想も複素解析に関連しているので,解析的整数論に関連して語られることが多いです.(とはいっても,正直私はそこまでよくわかってないです.)
初等整数論
正直,これといってじっくり細部まで読んだ本はないのですが,その中でも比較的よかった本を紹介します.
雪江 明彦:整数論1 初等整数論からp進数へ
この方面の人なら必ず知っている,雪江先生の本ですね.特徴としては,通常の整数についての合同や平方剰余の相互法則,不定方程式,連分数など,整数論の基礎としては主流のことが書いてある,群・環・環上の加群・体とGalois理論などの(そこまで深くはないが必要なレベルまでの)章が設けられている,代数的整数や$p$進数など,代数的整数論へ向かう準備がしっかりされている,という点です.
これらを踏まえると,将来は代数的整数論を勉強したいけど代数学の知識があまり身に付いていない人,整数論とはどのようなモチベーションでどのようなことをやるのか興味のある人,におすすめです.章ごとに話の内容(扱う題材)や難易度が異なり,初めの方だけやってみるのもありだと思うので,幅広い年代の方におすすめできます.高校生でも,進学校の高校の生徒であればゼミなどで全然扱えるレベルだと思います.
高木 貞治:初等整数論講義 第2版
次は,整数論をやっていて知らない人はいない,高木先生の初等整数論講義です.高木先生は類体論という理論の創設者です.ちなみに,類体論は(高木先生の創った古典的なものはあまり学ばないかもしれませんが)代数的整数論の知識を前提に学ぶような内容です.
この本の特徴は,不定方程式と,二次体の整数論についての記述が豊富であるという点です.二次体とは,体の2次拡大体のことで,そこにおける整数論は,容易だが奥深い例を豊富に与えてくれます.そのため,代数的整数論を勉強するときは,まず二次体について色々考えてみることが多いです.
そのため,この本も将来は代数的整数論を勉強したいと思っている人におすすめです.ただ,分量が多いのと難しい内容が多いので,いきなり全てを読破するのは厳しいと思います.将来勉強していく中で何度も読み返すような使い方になりそうです.
青木 昇:素数と2次体の整数論 (数学のかんどころ 15)
先ほど二次体の話も出たのでこの本も紹介します.この本は正直,初学者にものすごくおすすめです.(共立出版のかんどころシリーズ,どれもいいですよね.)特徴としては,通常の整数についての性質が理解しやすいように書かれている,平方剰余の相互法則を証明まで含めて述べている(Gauss和による証明),自然にイデアルや既約剰余類群,二次体の整数環を定義しており,概念が理解しやすい,素イデアル分解やイデアル類群の応用まで述べられている,という点です.群・環・体の知識はある方がいいですが,それも付録で定義から紹介されています.ただ一つ注意すべきポイントは,記述や証明が二次体に特化しすぎて,一般の場合適用できないものがいくつかあります.
そのため,この本は初学者におすすめです.高校生でも意欲のある生徒なら読めると思います.そして,これを読んだ後にはしっかしとした代数的整数論の本で再度一般論を理解して欲しいと思います.
代数的整数論
代数的整数論についてはたくさんの本があり,それぞれいいところがあるので,まずは一冊ベースになる本(教科書というべき?)を決めて,周辺知識を他の本で埋めるという流れで勉強すると良いです.まずは教科書としておすすめな本を先に紹介します.
加藤 和也・黒川 信重・斎藤 毅:数論 I Fermatの夢と類体論
この本は圧倒的に有名です.私もこの本を教科書として読みまくりました.構成としては,楕円曲線や二次曲線の有理点の話や,$p$進数体の構成,不定方程式,Fermatの最終定理など,整数論の素養が広がる話から始まり,代数的整数論,$\zeta$関数,イデアルの分岐理論,類体論についての話など,正統派の流れで盛りだくさんの内容です.良いポイントとして,いきなり難しい話をするのではなく,類体論の内容でも概要を掴むための簡単な章と,主定理のステートメントと証明をしっかり理解する章とで分けてあって,順に読むことで理解しやすい構成になっている点です.
ちなみに,この本では類体論はアデール・イデールを用いて定式化しています.そこの知識もきちんと説明してくれています.また,この手の議論で必要となる位相群の知識も,(証明は抜きにして)比較的述べられているように思います.(他の類体論の本では,位相群の知識を平然と使っていることが多いです.)
注意すべき点としては,次の本のところでも述べますが,全体的なテーマとして代数体における類体論の応用があるので,1変数代数関数体についてはあまり扱っていません.(大域体についての命題の証明も,代数体の場合しか書かれていないこともあります.)
そのため,この本は,群・環・環上の加群・体とGalois理論などの代数学の知識はある程度勉強済みで,整数論をやってみたいという人,類体論の勉強をしてみたいという人,におすすめです.
森田 康夫:整数論
この本は,教科書や辞書として使いたい本です.私は,色々な知識を埋めるための辞書として使っています.特徴としては,記述がしっかりとしているという点です.有限体,Dedekind環などの整数論で用いられる代数学の知識を,しっかりと述べています.また,付値論から局所体や大域体をしっかり構成している点が特徴です.上で紹介した数論I(加藤・黒川・斉藤)では付値論を詳しくやらず,局所体と大域体の定義をそこまで厳密にはやっていません.さらに,1変数代数関数体についての記述が豊富です.数論Iでは代数体において類体論を応用することが一つのテーマだったので,1変数代数関数体についてはあまり詳しくなかったので,嬉しいですね.ただ,この本は類体論についての記述がほとんどない(本当に紹介程度)ので注意してください.
そのためこの本は,整数論をやってみたい人がいきなり教科書にするのではなく,辞書のような感じで使うのが良いと思います.しかし,持っていて必ず損はないと思います.
山本 芳彦:現代数学への入門 数論入門
この本は,初学者向けの教科書といった感じです.先ほど紹介した数論I(加藤・黒川・斉藤)よりも簡単な(というか丁寧に書かれている)内容になっていると思います.内容としては,初等整数論で紹介した本にあるような内容(合同式や剰余環,既約剰余類群,平方剰余の相互法則など)から始まり,二次体や代数体の整数論を数論Iと同程度(もしくはそれより少し基礎的に)展開して,楕円モジュラー関数や楕円曲線などの虚数乗法論についての話に行きます.
整数論を展開する際,UFD,PIDなど環論の知識も紹介しながら書かれているため,代数学の知識にあまり自信がない人も読めると思います.数論Iの知識の補足としても使えると思います.
藤﨑 源二郎:代数的整数論(上・下)
これも名著です.上巻では群・環・体・Galois理論などの代数学からの準備,代数体についての全般的な理論が述べてあり,下巻では相対代数体についての全般的な理論と様々な例が述べられています.上下巻を通して,self-containdで,痒いところに手が届き,具体例がとても豊富であるというイメージがあります.例えば,上巻においては整数論において必要な環論の知識を,必要になった時に定義したり,下巻には3次体や双2次体についての色々な計算方法なども述べられています.
そのため,線形代数などの教養レベルの学習を終え,代数的整数論の勉強を始める際に教科書として使える本だと思います.ただし,初等整数論によく出る内容はほとんど触れられていないのと,書き方が数論I(加藤・黒川・斎藤)や数論入門(山本)の岩波書店のものよりも少し数学書チックなので,数学書の読み方にある程度慣れている人でないと難しいかもしれません.そのため,理学部数学科のB2,B3で,授業で代数学を学び始め,もしくは学び終えるくらいの人に一番おすすめです.
雪江 明彦:整数論2 代数的整数論の基礎
先ほど紹介した「整数論1初等整数論からp進数へ」の続編です.この本は,正直,初めに手にとる教科書にはおすすめしません.逆に,辞書や参考書として,とても良いと思います.雪江先生のシリーズは,シリーズものでこと細かな内容まで触れられている一方で,分量が多く,書き方も独特です.なので,(代数学シリーズの1,2,3と整数論の1を読んできた人以外は)一冊目にやる本としては,他の本の方が優れていると思います.しかし,豊富な内容なため,非常に参考になります.技術的なことでお世話になることが多いイメージです.
さらに類体論を勉強したい人へ
代数的整数論を学ぶための本としては,上で挙げたものをお勧めしますが,さらに進んで類体論を勉強したい方向けの本を紹介します.
先ほど紹介した「数論 I Fermatの夢と類体論」(加藤・黒川・斎藤)は,まず教科書としてお勧めです.それに加えて参考書として考えれるのが,以下です.
高木 貞治:代数的整数論
類体論を専門にする人は一度は読んでおくべきと言われる名著です.前半は代数的整数論の一般論,後半は類体論(高木先生の創り上げた古典的類体論)について述べてあります.
足立 恒雄・三宅 克哉:類体論講義
教科書としても良いと思います.論理展開が現代的で,読みやすいと思います.後半は類体論の歴史について書いてあります.
彌永 昌吉:数論
群のcohomologyから始めて,類体論をcohomology的に記述しています.類体論の歴史も付録に述べられており,非常にまとまっています.
さいごに
代数的整数論は奥深い理論で,僕自身まだまだ知らないことが多いです.今後もいろんな本を読んで勉強して,いずれ代数的整数論についてまとめたノートを作りたいと思います.
同様のおすすめ本を紹介する記事の,代数学編はこちらです.もしよかったら参考にしてください.

































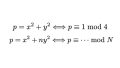
コメント