今回は、高等学校で学ぶ「数学的帰納法」の考え方と、理工学で使われている様々な帰納法についてお話しします。
はじめに
数学的帰納法を習ったばかりの人(高2が多いかな?)は、「雰囲気は分かったけど、実際どう書いたらいいか分からない」という現象が起きているかもしれません。そして、証明の記述を暗記してしまうようになってしまいます。そういう人は、この記事を通して数学的帰納法を理解して疑問を解消していってもらえると嬉しいです。
また、記事の最後のにある「様々な帰納法」は、大学などで学ぶ内容ですので、興味のある人は見てみてください。
※この記事では、高校生向けであることを考慮して、0は自然数ではないとしています。
数学的帰納法の基礎
帰納と演繹
数学的帰納法の「帰納」とは何かを説明します。
きのう【帰納】(induction)推理・思考の手続きの一つ。個々の具体的な事柄から、一般的な命題や法則を導き出すこと。「―法」えんえき【演繹】(deduction)普遍的命題から特殊命題を導き出すこと。一般的に、組み立てた理論によって、特殊な課題を説明すること。
このように日常の言葉としてもよく使われます。
帰納的な考え方は、例えば「A君は眠る。B君も眠る。C君も…したがって、すべての人間は眠るだろう」と導くことです。
演繹的な考え方は、例えば「すべての人間は眠る(ことが分かっている)。したがってA君は眠るし、B君も眠るし、C君も…」と説明することです。
数学的帰納法は、「帰納」的な要素を持った証明方法です。
高校で習う数学的帰納法
高校では、数学的帰納法をこのように習うと思います。
全ての自然数nについて成立することを証明するとき、
(i)n=1のときを証明
(ii)n=kのときを仮定し、n=k+1のときを証明
すればよい
数学的帰納法の基本はこれです。
厳密な理論は後ほど述べますが、まずはこれをマスターすることが目標です。
イメージは、「ドミノ倒し」です。
一番初めの自然数である1のとき成立することを確認(一番初めのドミノが倒れることを確認)する。その後、あるkのとき成立することを仮定(あるどこかのドミノが倒れた時を仮定)したときに、その次の自然数k+1も成立することを確認(次のドミノも倒れることを確認)する。これらにより、すべての自然数について成立する(すべてのドミノが倒れる)ことが示される。
ということです。
数学的帰納法は本当に帰納的なのか
数学的帰納法を初めて習ったとき、当時高校2年生だった私は、「数学的帰納法って、帰納的ではあるけど、演繹的でもあるのではないか?」と思いました。
どういうことかというと、「『○○(命題)を証明せよ』といっている段階で、その命題が正しいことは分かっているのだから、その命題に対してすべての自然数nについて成立することを示す行為は、演繹的だろ!!」ということです。
この疑問は、帰納と演繹を知っている人なら誰でも考えることだと思います。
そして私は、この疑問に対して、このように納得し解決しました。
・「証明せよ」というのは、数学の問題にするための表記として「(真か偽かはまだ不明だとして、)証明がもしできるならそれを試みよ」といっているのであって、まだ真だといったわけではない。
・本質は、自然数が連続していくことを利用して、無限に大きい自然数のときも成立することを示せる「帰納的」な考え方である。
しかし、やはり数学的帰納法は、本来の帰納法とはニュアンスが若干違います。なので、しっかりと「数学的」帰納法と表記することが必要です。
数学的帰納法の理論
理論をお話ししますが、少し難しいので、高校生の初学者は飛ばしてもらっても構いません。細かく理解したい人や、受験生は軽く見てみてください。
数学的帰納法①
上で述べた「高校で習う数学的帰納法」を厳密に書くと、このような(真なる)命題になります。
自然数上の命題関数P(n)が以下を満たすとする。
・P(0)が成立する。
・P(n)が成立するならばP(n+1)も成立する。
このとき、すべての自然数nについてP(n)が成立する。
命題関数とは、命題(真偽が確定できる文)の中に変数を組み込み、変数の値ごとに真偽が定まるような文です。
例えば、「xは5より小さい(ただしxは実数)」という命題関数は、x=1のときは真ですが、x=6のときは偽です。
「成立する」というのは、その命題(命題関数)が真であることを意味しています。
(この「数学的帰納法①」という命題は、自然数の整列性を用いて証明できます。それを数学的帰納法として利用しているのです。大学内容なので証明は省略します。)
数学的帰納法②(累積帰納法)
実は、前述の数学的帰納法①を拡張した、広い意味での数学的帰納法があります。それは、「累積帰納法」と呼ばれ、以下の(真なる)命題です。
自然数上の命題関数P(n)が以下を満たすとする。
・すべてのm(<n)でP(m)が成立するならばP(n)も成立する。
このとき、すべての自然数に対してP(n)が成立する。
前述の数学的帰納法①では、一つ前の自然数のとき成立することを仮定していましたが、この累積帰納法では、以前のすべての自然数のとき成立することを仮定しています。
また、n=1のときはこれをm<nを満たす自然数mは存在しないので、前提部の「すべてのm(<n)でP(m)が成立する」は自動的に真と解釈されます。(高校ではあまり教えてくれませんが、Aが偽のときは「AならばB」は(Bの真偽に関わらず)真になります。)
これより、累積帰納法は、数学的帰納法①を含んでいる広いものであることが分かります。
高校生の問題でも、仮定が2つ以上必要な場合や、前のすべてを仮定する必要がある場合があります。それはまさに、この累積帰納法を使っているのです。
数学的帰納法の注意点・よくある間違い
まず、この答案を見てください。どこが間違っていると思いますか?
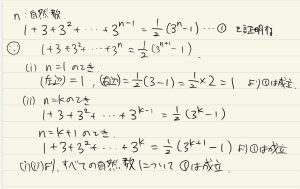
示すべき内容は初めに書かない!
これは、数学的帰納法だけでなく、すべての証明にいえることです。頭の隅に置いておくか、答案の隅にメモするくらいならいいでしょう。
仮定を用いる!
n=k+1のときの式を導くときは、必ずn=kのときに成立するという仮定を用いてください。そうしないと、論理が崩壊してしまいます。
「=」の意味を区別する
同値変形(式変形)をした「=」、仮定を用いた「=」、示すべき「=」をしっかりと区別できるようにしてください。
これらを修正した、正しい答案がこれです。

その他の帰納法
構造帰納法
計算機科学などの分野に導入されているデータ構造は、帰納的に定義されていることがあります。このようなデータ構造の性質は、それに従った帰納法で証明することができます。このような帰納法を「構造帰納法(structural induction)」といいます。
例としては、二分木上の構造帰納法などがあります。
ネーター帰納法
最も一般的な帰納法として、「ネーター帰納法(Neotherian induction)」または「整礎帰納法(well-founded induction)」と呼ばれる帰納法があります。
これは、整礎順序という大学内容の概念を使っているので、ここでは細かく説明できないため割愛します。
このように、高校で習う数学的帰納法以外にも、様々な帰納法があります。興味のある人は是非調べてみてください。


コメント