今回はタイトルの通り,フェルマー(Fermat)の二平方和定理に関連する内容を考えていきます.
フェルマーの二平方和定理とは,「素数$p$がある整数$x,y$を用いて$p=x^2+y^2$の形で書けることは,$p=2$もしくは$p$が$4$で割って$1$余る(すなわち$p \equiv 1 \bmod 4 $である)素数であることと同値である.」という主張です.
具体例としては,
$2=1^2+1^2$は明らかだとしても,
$5=1^2+2^2$
$13=2^2+3^2$
$17=1^2+4^2$
のように,$4$で割って$1$余る奇素数はこのように書けます.
一方で,$3,7,11,19,\cdots$のように,$4$で割って$3$余るような素数は,どんなに考えても$p=x^2+y^2$($x,y \in \mathbb{Z}$)のようには表せません.
この記事では,この問題を「平方剰余記号」という初等整数論において基本的な道具と,環論の基礎知識を用いて証明するとともに,少し条件を変えて,色々な$n$に対して「ある整数$x,y$を用いて$p=x^2+ny^2$」と書ける素数の判定について考えていきます.
いくつかの結論
まず,いくつかの結論を先に述べることにします.なお,フェルマーの二平方和定理のときの$p=2$のような,$p \equiv △ \mod ○$の条件とは関係ない素数は,実は有限個であることが証明されており,個別に考えれば良いので,先に排除しておくようにしておきます.そのような素数がどのようなものかについてもいずれ述べようと思います.
$p$を2でない素数とする.このとき,$p=x^2+y^2$ となる $x,y \in\mathbb{Z} $ が存在することと,$p$が$4$で割ると$1$余ること(すなわち$p \equiv 1 \bmod 4$)は同値である.
$p$は2でない素数とする.このとき,$p=x^2+2y^2$ となる $x,y \in\mathbb{Z} $ が存在すること,$p$が$8$で割ると$1$または3余ることと(すなわち$p \equiv 1,3 \bmod 8$)は同値である.
$p$は3でない素数とする.このとき,$p=x^2+3y^2$ となる $x,y \in\mathbb{Z} $ が存在することと,$p$が$3$で割ると$1$余ること(すなわち$p \equiv 1 \bmod 3$)は同値である.
ここまで流れ的には,「どんな$n$に対しても$p=x^2+ny^2$と表せるための美しい条件があるのでは?」と思いますが,実はそうではありません.例えば下の結論のように,$n$によっては,このような$p \equiv △ \mod ○$の形の判定法がないことが証明されています.
$p=x^2+26y^2$ となる $x,y \in\mathbb{Z}$ が存在する$p$の条件を,$p \equiv △ \bmod ○$の形で判定することはできない.
このことは,類体論という内容の知識が必要になります.この記事の最後の方で,再度簡単に紹介します.
いくつかの前提知識
証明を行うために必要ないくつかの前提知識について述べていきます.細かくは説明しないので,見覚えのない方は整数論や環論(代数学)の文献などを少し眺めてみることをお勧めします.
まずは,平方剰余記号(Legendre記号)です.これは初等整数論の内容として,広く知られています.
奇素数$p$と,$p$で割れない整数$a$に対して,
\begin{align*}
\displaystyle \left( \frac{a}{p} \right) &=
\begin{cases}
1 & (x^2 \equiv a \bmod p となるx \in \mathbb{Z}が存在する) \\
-1 & (x^2 \equiv a \bmod p となるx \in \mathbb{Z}が存在しない)
\end{cases}
\end{align*}
と定める.これを,平方剰余記号またはLegendre記号という.
平方剰余記号には以下の性質があります.
(乗法性)$a,b$を$p$で割れない整数とするとき,
\begin{align*}
\displaystyle \left( \frac{ab}{p} \right) = \left( \frac{a}{p} \right) \left( \frac{b}{p} \right)
\end{align*}
(平方剰余の相互法則)$q$を$p$と異なる奇素数とするとき,
\begin{align*}
\displaystyle \left( \frac{q}{p} \right) = (-1)^{\frac{p-1}{2}} (-1)^{\frac{q-1}{2}} \left(\frac{p}{q} \right)
\end{align*}
(第一補充法則)
\begin{align*}
\displaystyle \left( \frac{-1}{p} \right) = (-1)^{\frac{p-1}{2}}
\end{align*}
(第二補充法則)
\begin{align*}
\displaystyle \left( \frac{2}{p} \right) = (-1)^{\frac{p^2-1}{8}}
\end{align*}
これらの性質の証明は様々な方法がありますが,この記事では省略します.(多分ググったら簡単に出てきます.)この性質の中でも,第一補充法則を後に使います.
さて,次は代数学の環論からの知識です.「素元」の定義を再確認しておきます.
整域$A$の元$\alpha$が$A$の素元であるとは,以下の$2$つの条件を満たすことである.
- $\alpha$は$0$でも$A$の可逆元でもない.
- $a,b \in A$かつ$ab \in \alpha A = \{ \alpha x | x \in A \}$ならば,$a \in A$または$b \in A$である.
また,素元分解整域の定義を再確認しておきます.
整域$A$が素元分解整域であるとは,次の2つの条件を満たすときをいう.
- $A$の0でも可逆元でもない元$\alpha$は$\alpha = a_1\cdots a_k$($k \ge 1,a_1, \cdots a_k $は$A$の素元)と表せる.
- $\alpha = a_1\cdots a_k$かつ$\alpha = b_1\cdots b_l$($k,l \ge 1,a_1, \cdots, a_k,b_1, \cdots ,b_l $は$A$の素元)ならば,$k=l$であり$b_1, \cdots b_l$の番号を付け替えれば$i=1, \cdots ,k$に対して$b_i=a_i \times $($A$の可逆元)とできる.
なお,素元分解整域は一意分解整域(Unique Factorization Domain,UFD)とも言われます.文献によって,この2つの定義が異なる場合がありますが,実は同じものです.
結論①(フェルマーの二平方和定理)の証明
さて,早速フェルマーの二平方和定理の証明をしていきましょう.実は,定理の同値のうち
「$p=x^2+y^2$ となる $x,y \in\mathbb{Z} $ が存在する $\Longrightarrow$ $p \equiv 1 \bmod 4$」の方はとても簡単に示すことができます.それは次のように示されます.
$x,y \in \mathbb{Z}$が$p=x^2+y^2$を満たすとする.$x,y$がともに偶数,もしくはともに奇数であれば,$x^2+y^2$は偶数であり,$p=x^2+y^2$が奇素数であることに矛盾する.よって,$x,y$のどちらか一方が奇数でもう一方が偶数である.$x$を偶数,$y$を奇数としてよい.このとき$x=2n , y=2m+1$となる$n,m \in \mathbb{Z}$が存在し,$p=x^2+y^2=4(n^2+m^2+m)+1 \equiv 1 \bmod 4$である.
一方で,「$p=x^2+y^2$ となる $x,y \in\mathbb{Z} $ が存在する $\Longleftarrow$ $p \equiv 1 \bmod 4$」の方は先程確認した様々な知識が必要です.
証明のポイントとしては,$x^2+y^2=(x+y\sqrt{-1})(x-y\sqrt{-1})$であることと,($\mathbb{Q}$に$\sqrt{-1}$を添加した代数体$\mathbb{Q}(\sqrt{-1})$の整数環である)環$\mathbb{Z}[\sqrt{-1}]$がUFDであることを用いています.
$p$を4で割ると1余る素数であるとする.$\alpha = x+y\sqrt{-1} \in \mathbb{Z}[\sqrt{-1}]$とすると$\alpha \overline{\alpha} = (x+y\sqrt{-1})(x-y\sqrt{-1}) =x^2+y^2$であるから,$p=\alpha \overline{\alpha}$となる$\alpha \in \mathbb{Z}[\sqrt{-1}]$が存在することを示せば良い.
$p-1$は4の倍数であるから$\displaystyle \frac{p-1}{2}$は偶数であり,第一補充法則より$\displaystyle \left( \frac{-1}{p} \right) = 1 $である.すなわち,$a^2 \equiv -1 \bmod p$となる$a \in \mathbb{Z}$が存在する.$a^2+1 \equiv 0 \bmod p$より$a^2 +1 = (a+\sqrt{-1})(a-\sqrt{-1}) \in p\mathbb{Z}[\sqrt{-1}]$ であり,$a+\sqrt{-1},a-\sqrt{-1} \notin p\mathbb{Z}[\sqrt{-1}]$であるから$p$は$\mathbb{Z}[\sqrt{-1}]$の素元ではない.また,$p$は$\mathbb{Z}[\sqrt{-1}]$の可逆元ではない.($\mathbb{Z}[\sqrt{-1}]$の可逆元は$\pm 1,\pm \sqrt{-1}$のみである.)
$\mathbb{Z}[\sqrt{-1}]$はUFDであるから,$p$の$\mathbb{Z}[\sqrt{-1}]$での素元分解を考えることにより,ある$\mathbb{Z}[\sqrt{-1}]$の素元$\alpha$と可逆元でない元$\beta$があって$p=\alpha \beta$となる.($\beta \in \mathbb{Z}[\sqrt{-1}]$が可逆元でないのは,$p$が素元でないことから分かる.)このとき,$p^2=\alpha \beta \overline{\alpha \beta} = \alpha \overline{\alpha} \beta \overline{\beta}$であり,$\alpha \overline{\alpha} ,\beta \overline{\beta} \in \mathbb{N}$であるから,$\alpha \overline{\alpha}$は$1,p,p^2$のいずれかである.$\alpha \overline{\alpha} =1,p^2$なら,それぞれ$\alpha,\beta$が可逆元でないことに反するので,$\alpha \overline{\alpha} =p$である.
結論②の証明
先程と同様に,$2$でない素数$p$に対して「$p=x^2+2y^2$ となる $x,y \in\mathbb{Z} $ が存在する $\Longleftrightarrow$ $p \equiv 1,3 \bmod 8$」であることを示していきます.方針などはフェルマーの二平方和定理のときと全く同じです.
$x,y \in \mathbb{Z}$が$p=x^2+2y^2$を満たすとする.$x$が偶数であれば$x^2+2y^2$は偶数であり,$p=x^2+2y^2$が奇素数であることに矛盾する.よって$x$は奇数である.$y$が偶数のとき,$x=2n+1 , y=2m$となる$n,m \in \mathbb{Z}$が存在し,$p=x^2+2y^2=4n(n+1)+1+8m^2 \equiv 1 \bmod 8$である.$y$が奇数のとき,$x=2n+1 , y=2m+1$となる$n,m \in \mathbb{Z}$が存在し,$p=x^2+2y^2=4n(n+1)+1+8m^2+8m+2 \equiv 3 \bmod 8$である.
$p$を8で割ると1または3余る素数であるとする.$\alpha = x+y\sqrt{-2} \in \mathbb{Z}[\sqrt{-2}]$とすると$\alpha \overline{\alpha} = (x+y\sqrt{-2})(x-y\sqrt{-2}) =x^2+2y^2$であるから,$p=\alpha \overline{\alpha}$となる$\alpha \in \mathbb{Z}[\sqrt{-2}]$が存在することを示せば良い.
$p \equiv 1 \bmod 8$のとき,$\displaystyle \frac{p-1}{2}$と$\displaystyle \frac{p^2-1}{8}$はともに偶数であり,平方剰余記号の性質より$\displaystyle \left( \frac{-2}{p} \right) = \left( \frac{-1}{p} \right) \left( \frac{2}{p} \right) = 1 $である.また,$p \equiv 3 \bmod 8$のとき,$\displaystyle \frac{p-1}{2}$と$\displaystyle \frac{p^2-1}{8}$はともに奇数であり,同様に$\displaystyle \left( \frac{-2}{p} \right) = \left( \frac{-1}{p} \right) \left( \frac{2}{p} \right) = 1 $である. すなわち,$a^2 \equiv -2 \bmod p$となる$a \in \mathbb{Z}$が存在する.$a^2+2 \equiv 0 \bmod p$より$a^2 +2 = (a+\sqrt{-2})(a-\sqrt{-2}) \in p\mathbb{Z}[\sqrt{-2}]$ であり,$a+\sqrt{-2},a-\sqrt{-2} \notin p\mathbb{Z}[\sqrt{-2}]$であるから$p$は$\mathbb{Z}[\sqrt{-2}]$の素元ではない.また,$p$は$\mathbb{Z}[\sqrt{-2}]$の可逆元ではない.($\mathbb{Z}[\sqrt{-2}]$の可逆元は$\pm 1$のみである.)
$\mathbb{Z}[\sqrt{-2}]$はUFDであるから,$p$の$\mathbb{Z}[\sqrt{-2}]$での素元分解を考えることにより,ある$\mathbb{Z}[\sqrt{-2}]$の素元$\alpha$と可逆元でない元$\beta$があって$p=\alpha \beta$となる.このとき,$p^2=\alpha \beta \overline{\alpha \beta} = \alpha \overline{\alpha} \beta \overline{\beta}$であり,$\alpha \overline{\alpha} ,\beta \overline{\beta} \in \mathbb{N}$であるから,$\alpha \overline{\alpha}$は$1,p,p^2$のいずれかである.$\alpha \overline{\alpha} =1,p^2$なら,それぞれ$\alpha,\beta$が可逆元でないことに反するので,$\alpha \overline{\alpha} =p$である.
結論③の証明
$3$でない素数$p$に対して「$p=x^2+3y^2$ となる $x,y \in\mathbb{Z} $ が存在する $\Longleftrightarrow$ $p \equiv 1 \bmod 3$」であることを示していきます.
ちなみに,この証明では,($\mathbb{Z}[\sqrt{-3}]$はUFDではなく)$\mathbb{Z}[\zeta_3]$がUFDであることを用いるため,これまでの証明と少し工夫が必要です.証明するための補題を一つ示しておきます.
$\mathbb{Z}[\zeta_3]$の任意の元$\alpha$に対して,$\epsilon \alpha \in \mathbb{Z}[\sqrt{-3}]$となる$\epsilon \in \{1, \zeta_3 , \zeta_3^2 \} \subset \mathbb{Z}[\zeta_3]^{\times}$が存在する.
【証明】
$\displaystyle \mathbb{Z}[\zeta_3] = \left\{ \frac{k+l\sqrt{-3}}{2} \ \middle| \ k \equiv l \bmod 2 \right\}$であることが容易にわかる.$\displaystyle \alpha = \frac{k+l\sqrt{-3}}{2} \quad (k \equiv l \bmod 2)$とおく.$k \equiv l \equiv 0\bmod 2$なら,$\alpha \in \mathbb{Z}[\sqrt{-3}]$である.$k \equiv l \equiv 1 \bmod 2$なら,$k \equiv l \bmod 4$または$k \equiv -l \bmod 4$である.
$k \equiv l \bmod 4$のとき,$k+3l , k-l \in 4\mathbb{Z}$より,
\begin{align*}
\zeta_3^2 \alpha=\frac{-1+\sqrt{-3}}{2} \cdot \frac{k+l\sqrt{-3}}{2} =\frac{-(k+3l)+(k-l)\sqrt{-3}}{4} \in \mathbb{Z}[\sqrt{-3}]
\end{align*}
$k \equiv -l \bmod 4$のとき,$-k+3l , k+l \in 4\mathbb{Z}$より,
\begin{align*}
\zeta_3 \alpha=\frac{-1-\sqrt{-3}}{2} \cdot \frac{k+l\sqrt{-3}}{2} =\frac{-k+3l-(k+l)\sqrt{-3}}{4} \in \mathbb{Z}[\sqrt{-3}]
\end{align*}
である.
この補題を用いて,結論③を証明しよう.
$p=2$ のとき,$p=x^2+3y^2$ となる $x,y \in\mathbb{Z} $ が存在しないことは明らかである.なので$p \neq 2$とする.$x,y \in \mathbb{Z}$が$p=x^2+3y^2$を満たすとする.$x,y$がともに偶数,もしくはともに奇数であれば,$x^2+3y^2$は偶数であり,$p=x^2+3y^2$が奇素数であることに矛盾する.よって,$x,y$のどちらか一方が奇数でもう一方が偶数である.$x$が偶数で$y$が奇数のとき.$x=2n , y=2m+1$となる$n,m \in \mathbb{Z}$が存在し,$p=x^2+3y^2=4n^2+3(4m^2+4m+1) \equiv n^2 \bmod 3$である.もし$n$が3の倍数なら$p$は3の倍数となってしまうので,$n$は3の倍数でない.よって$n \equiv 1,2 \bmod 3$であり,いずれの場合にも$p \equiv n^2 \equiv 1 \bmod 3$である.$x$が奇数で$y$が偶数のとき.$x=2n+1 , y=2m$となる$n,m \in \mathbb{Z}$が存在し,$p=x^2+3y^2=4(n^2+n)+1+12m^2 \equiv n^2+n+1 \bmod 3$である.もし$x$が3の倍数なら$p$は3の倍数となってしまうので,$x$は3の倍数でない.このとき$n \equiv 0,2 \bmod 3$であり,いずれの場合にも$p \equiv n^2+n+1 \equiv 1 \bmod 3$である.
$p$を3で割ると1余る素数であるとする.$\gamma = x+y\sqrt{-3} \in \mathbb{Z}[\sqrt{-3}]$とすると$\gamma \overline{\gamma} = (x+y\sqrt{-3})(x-y\sqrt{-3}) =x^2+3y^2$であるから,$p=\gamma \overline{\gamma}$となる$\gamma \in \mathbb{Z}[\sqrt{-3}]$が存在することを示せば良い.
平方剰余記号の性質より,$\displaystyle \left( \frac{-3}{p} \right) = \left( \frac{-1}{p} \right) \left( \frac{3}{p} \right) = \left( \frac{-1}{p} \right) (-1)^{\frac{p-1}{2}} (-1)^{\frac{3-1}{2}} \left( \frac{p}{3} \right) = \left( \frac{p}{3} \right) =1$である.
すなわち,$a^2 \equiv -3 \bmod p$となる$a \in \mathbb{Z}$が存在する.$a^2+3 \equiv 0 \bmod p$より$a^2 +3 = (a+\sqrt{-3})(a-\sqrt{-3}) \in p\mathbb{Z}[\zeta_3]$ であり,$a+\sqrt{-3},a-\sqrt{-3} \notin p\mathbb{Z}[\zeta_3]$であるから$p$は$\mathbb{Z}[\zeta_3]$の素元ではない.また,$p$は$\mathbb{Z}[\zeta_3]$の可逆元ではない.($\mathbb{Z}[\zeta_3]$の可逆元は$\pm 1,\pm \zeta_3,\pm \zeta_3^2$のみである.)
$\mathbb{Z}[\zeta_3]$はUFDであるから,$p$の$\mathbb{Z}[\zeta_3]$での素元分解を考えることにより,ある$\mathbb{Z}[\zeta_3]$の素元$\alpha$と可逆元でない元$\beta$があって$p=\alpha \beta$となる.このとき,$p^2=\alpha \beta \overline{\alpha \beta} = \alpha \overline{\alpha} \beta \overline{\beta}$であり,$\alpha \overline{\alpha} ,\beta \overline{\beta} \in \mathbb{N}$であるから,$\alpha \overline{\alpha}$は$1,p,p^2$のいずれかである.$\alpha \overline{\alpha} =1,p^2$なら,それぞれ$\alpha,\beta$が可逆元でないことに反するので,$\alpha \overline{\alpha} =p$である.上で述べた補題より,ある$\epsilon \in \{1, \zeta_3 , \zeta_3^2 \}$があって,$\epsilon \alpha \in \mathbb{Z}[\sqrt{-3}]$となる.$\gamma = \epsilon \alpha $とすれば,$p=\alpha \overline{\alpha}=\epsilon \overline{\epsilon} \alpha \overline{\alpha} = \gamma \overline{\gamma}$となる.
考察と,更なる問題
ここまでの結論①〜③の証明のポイントとして重要であったのは,$\mathbb{Z}[\sqrt{-1}]$,$\mathbb{Z}[\sqrt{-2}]$,$\mathbb{Z}[\zeta_3]$がUFDであることでした.ちなみにこれらはそれぞれ,代数体(すなわち有理数体$\mathbb{Q}$の有限次拡大体)$\mathbb{Q}(\sqrt{-1})$,$\mathbb{Q}(\sqrt{-2})$,$\mathbb{Q}(\sqrt{-3})$の整数環と言われる環です.$x^2+ny^2=(x+y\sqrt{-n})(x-y\sqrt{-n})$であるから,$\mathbb{Q}$に$\sqrt{-n}$を添加した体$\mathbb{Q}(\sqrt{-n})$を考察していたのです.
なお,$\Longrightarrow$の証明に,平方剰余記号の性質を用いて,整数環において$p$が素元でないことを示しましたが,この部分は環論に知識だけでも証明することができます.(すなわち,平方剰余記号を知らなくても,証明できます.そもそも平方剰余記号の性質も環論を用いて容易に証明できます.)例えば,フェルマーの二平方和定理の場合,
\begin{align*}
\mathbb{Z}[\sqrt{-1}]/(p) \cong \mathbb{F}_p[x]/(x^2+1)
\end{align*}
より,$p$が素元であることと$x^2+1$が$\mathbb{F}_p[x]$で既約であることは同値であり,これは$x^2+1=0$が$\mathbb{F}_p$で解を持たないことと同値です.$p$が奇素数のときは$\mathbb{F}_p^{\times}$が位数$p-1$の巡回群になることから,これが$p \equiv 1 \bmod 4$と同値であることが容易にわかります.この方法については,雪江先生の代数学2にも載っています.(参考文献欄にリンクを置いておきます.)
代数的整数論の知識にはなりますが,代数体の整数環がUFDであることと,代数体の重要な値である「類数」というものが1であることは同値です.従って,類数が2以上である代数体では,ここまでの方法は使えません.その場合は,その代数体の(狭義の)Hilbert類体というものを考える必要があります.もっと詳しく言えば,素数$p$が$\mathbb{Q}(\sqrt{-n})$の(狭義の)Hilbert類体において「完全分解」することと,$p=x^2+ny^2$ となる $x,y \in\mathbb{Z} $ が存在することが同値になります.従って(狭義の)Hilbert類体を調べることに帰着することができます.
また,冒頭に紹介した,結論④「$p=x^2+26y^2$ となる $x,y \in\mathbb{Z}$ が存在する$p$の条件を,$p \equiv △ \bmod ○$の形で判定することはできない.」というのも,類体論を用いて証明できます.もっと詳しく言うと,$\mathbb{Q}(\sqrt{-26})$の(狭義の)Hilbert類体で完全分解する素数$p$を探せば良いのですが,実は素数$p$が代数体$L$で完全分解するか否かを$p \equiv △ \bmod ○$の形で判定するためには,$L$が$\mathbb{Q}$のAbel拡大(Galois群がAbel群)であることが必要十分条件となり,この事実と,$\mathbb{Q}(\sqrt{-26})$の(狭義の)Hilbert類体が$\mathbb{Q}$のAbel拡大ではないことによって,結論④が従います.
これらのことは,類体論という内容によって理解できる,非常に奥深い内容です.また機会があれば,もう少し詳しく紹介したいと思います.
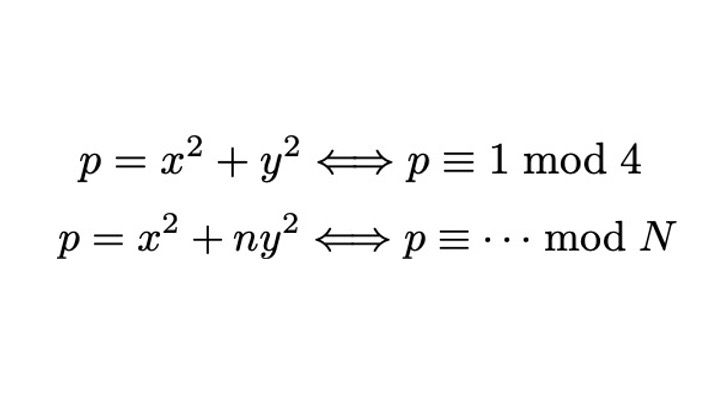







コメント