線形・非線形とは「非線形」ってナンセンス？

今回は、数学や物理でよく聞く「線形性（線型性）」について説明します。また、今まで学んできた内容の中で線形性があるものをご紹介します。

定義

$a,b,x,y$を任意の実数（もしくは複素数、ベクトルなど）とする。演算$L$が、$$L\left( ax+by\right) =aL\left( x\right) +bL\left( y\right) $$を満たすような性質を「線形性」といいます。

また、上の性質を分解して、$$L\left( x+y\right) =L\left( x\right) +L\left( y\right) \tag{1}$$$$L\left( ax\right) =aL\left( x\right) \tag{2}$$とする場合もあります。

この場合、性質$(1)$を「加法性」、性質$(2)$を「（演算との）可換性」ということもあります。

意味とイメージ

「線形（の）」は英語でlinearといいます。他の和訳は「線状の、直線の、リニア」です。

線形性を簡単に言うと、原点を通る直線のような性質です。

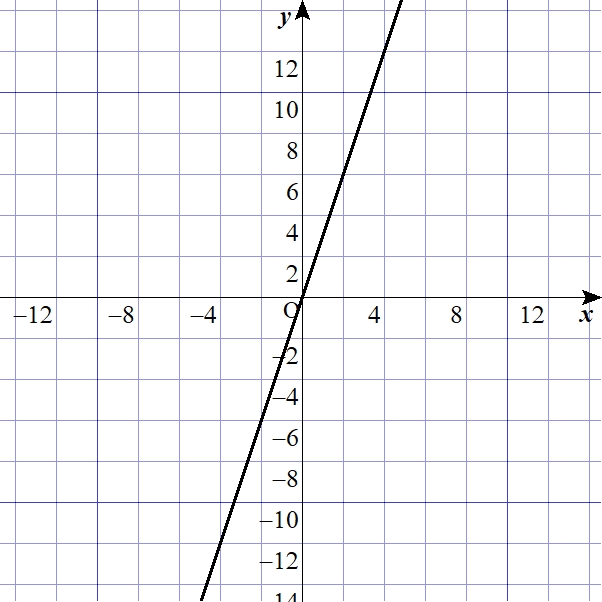
例えば、一次関数$f(x)=3x$を考えます。$y=f(x)$をグラフにすると、もちろんこのようになります。

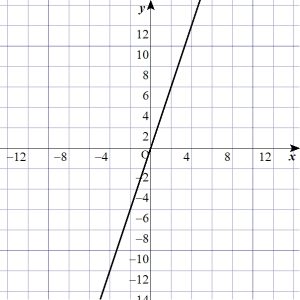
この関数に関して線形性があるかを確認してみます。

性質$(1)$については、

$\begin{eqnarray*}f\left( x+y\right) &=&3(x+y) \\
&=&3x+3y\\
&=&f\left( x\right) +f\left( y\right) \end{eqnarray*} $

となるため満たします。

性質$(2)$については、

$\begin{eqnarray*} f\left(ax\right) &=& 3(ax) \\ &=&a(3x) \\ &=&3f\left( x\right)　 \end{eqnarray*} $

となるため満たします。以上より、一次関数$f(x)=3x$は線形性がある（線形である）といえます。

しかし、例えば一次関数$f(x)=3x+1$は、実は線形ではありません。（線形ではないものを非線形といいます。）実際、

$\begin{eqnarray*}f\left( x+y\right) &=&3(x+y) +1\\
&=&3x+3y+1\\
&\ne&f\left( x\right) +f\left( y\right) \end{eqnarray*} $

となり、性質$(1)$を満たさないからです。

以上の議論より、線形性とは、原点を通る直線のような性質であることが分かります。

一次≒線形

先ほどの例では、”一次”関数は必ずしも”線形”ではないことが分かりました。

しかし、「一次」と「線形」という日本語があまり区別されていない用語もあります。

例えば、線形結合＝一次結合、線形独立(従属)＝一次独立(従属)、線形変換＝一次変換、などは、同じ意味を表します。

しかし、線形代数のことを一次代数とはいいません。

線形代数に関する記事はこちら：なぜ線形？線形代数とは　大学・高専の線形代数の全体像と流れ，参考書

線形性が見られる例

いわゆる「定数は外に出せる」と「項をそれぞれ演算すればよい」ということが見て取れます。

和の記号Σ（シグマ）

$$\sum ^{n}_{k=1}\left( ax_{k}+by_{k}\right) =a\sum ^{n}_{k=1}x_{k}+b\sum ^{n}_{k=1}y_{k}$$

総和を取るという演算子$Σ$は線形性を持っています。（高等学校数学B）

微分

$$\dfrac {d}{dt}\left( ax\left( t\right) +by\left( t\right) \right) =a\dfrac {d}{dt}x\left( t\right) +b\dfrac {d}{dt}y\left( t\right)$$

$t$は独立変数、$x,y$は$t$の関数です。微分演算子$\dfrac {d}{dt}$は線形性を持っています。（高等学校数学Ⅱ）

積分

$$\int ^{t_{2}}_{t_{1}}\left( ax\left( t\right) +by\left( t\right) \right) dt=a\int ^{t_{2}}_{t_{1}}x\left( t\right) dt+b\int ^{t_{2}}_{t_{1}}y\left( t\right) dt$$

$t$は独立変数、$x,y$は$t$の関数です。積分演算子$\int ^{t_{2}}_{t_{1}}dt$は線形性を持っています。（高等学校数学Ⅱ）

極限

$$\lim _{t\rightarrow \alpha }x\left( t\right) , \lim _{t\rightarrow \alpha }y\left( t\right) $$がともに収束するとき，
$$\lim _{t\rightarrow \alpha }\left( ax\left( t\right) +by\left( t\right) \right) =a\lim _{t\rightarrow \alpha }x\left( t\right) +b\lim _{t\rightarrow \alpha }y\left( t\right) $$

積分演算子$\lim$は線形性を持っています。（高等学校数学Ⅲ）

線形変換（一次変換）

$$A\left( a\overrightarrow {x}+b\overrightarrow {y}\right) =aA\overrightarrow {x}+bA\overrightarrow {y}$$

ベクトルに行列をかけるという演算は線形です。

（線形代数）

線形微分方程式

線形微分方程式$x^{\left( n\right) }+p_{n-1}(t) x^{\left( n-1\right) }+\ldots +p_{1}(t) x’+p_{0}(t) x=r\left( t\right) $の左辺を$L(x)$とすると

$$L\left( ax_{1}+bx_{2}\right) =aL\left( x_{1}\right) +bL\left( x_{2}\right) $$

$x_{1},x_{2}$は任意の未知関数です。線形微分方程式の左辺は線形性を持っています。（微分方程式論）

他にも、さまざまな分野で線形性は出現します。

非線形について

先ほども少し述べましたが、線形でないものを非線形といいます。こう聞くと、非線形は、”線形でない特別な場合”であると認識してしまいがちですが、実は逆で、数学や物理、日常生活での一般的な現象においては、ほとんどが非線形なのです。たとえば、ばねの伸びの変位と弾性力が比例するという「フックの法則」でも、変位が相当大きい所ではばねが伸び切ってしまい弾性力が落ちます。このように、線形性があると思い込んでいる現象においても、線形として扱える範囲や条件が限られてしまうのです。また、実際の現象をモデリングして得た（偏）微分方程式式などは、非線形の場合が非常に多いです。（流体力学における基礎方程式である、ナビエ–ストークス方程式なども、非線形の偏微分方程式です。3次元の場合のこの方程式は、解析的な解の存在や一意性がいまだ証明されていません。）

非線形な現象を科学する総称として「非線形科学（nonlinear science）」という言葉があるのですが、それに対して数学者のウラム（米、1909-1984）は、皮肉としてこう述べたといいます。